경사하강법(Gradient Descent) 파헤치기

경사하강법? 확률적 경사 하강법? 미니 배치?

헷갈리는 용어들에 대한 개념을 확실히 하고자 정리해본다.

0. 서론

머신러닝(딥러닝 포함)에서의 학습이란 목표값과 예측값의 오차를 최소화 하는 방향으로 모델의 파라미터들을 조정하는 자동화된 알고리즘을 수행하는 것

• 손실 함수(Loss Function)
  • 모델의 예측값 <-> 목표값 간의 차이를 계산 해주는 함수
  • ‘오차’가 무엇인지 정의하는 함수

결국, 머신러닝은 손실 함수 값이 최소화하는 방향으로 학습시키는 것이 목적

그럼 어떻게 손실 함수값을 최소화 시킬까?

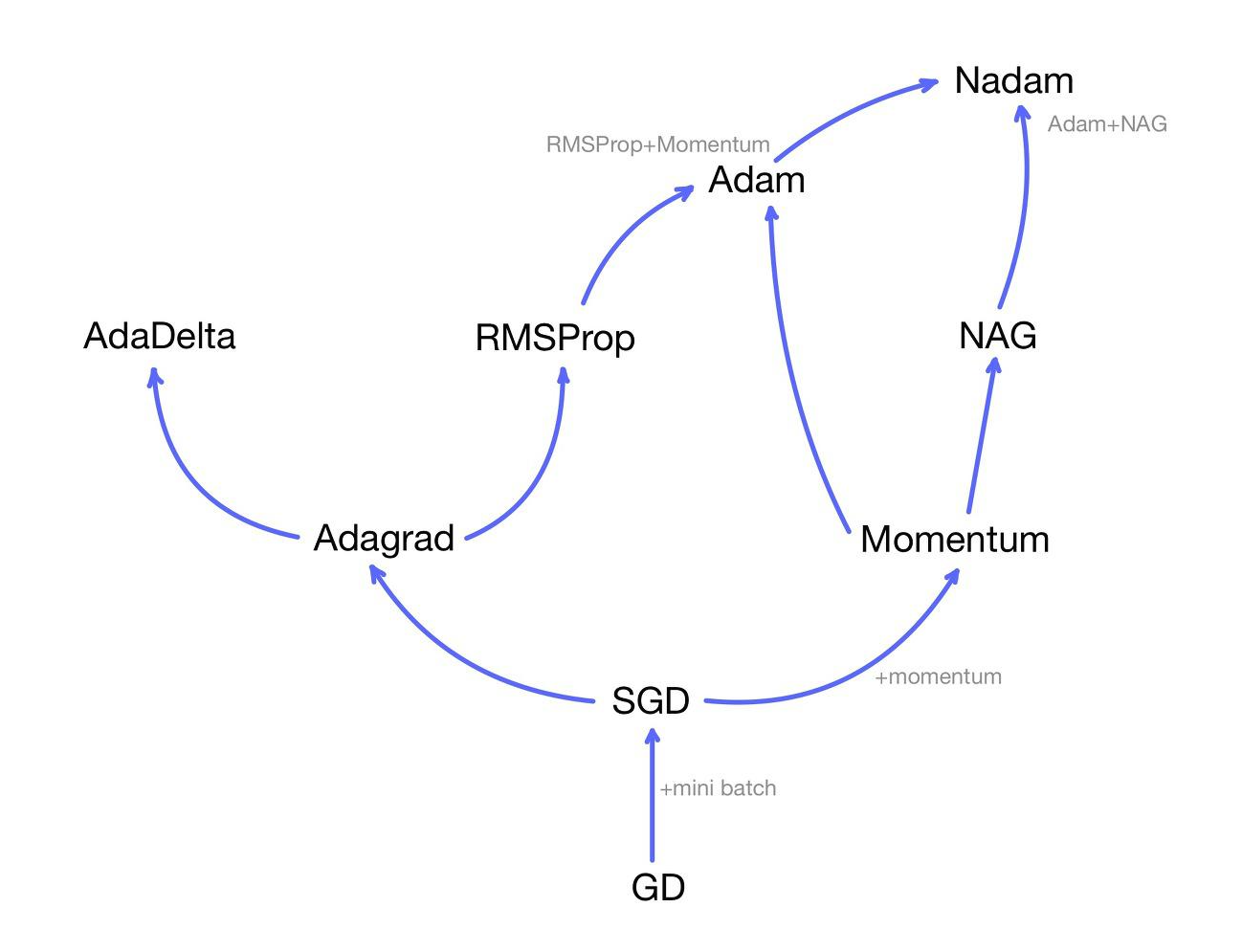
1. 옵티마이저 (Optimizer)

• 손실 함수 값을 최소화 한다 = 최적화 알고리즘을 수행한다 = 옵티마이저(Optimizer)

• GD = 경사 하강법(Gradient Descent)

• 최적화 알고리즘(옵티마이저): GD를 기본으로 하여 loss function이 최소가 되는 지점, 즉 최적의 가중치를 찾는 방법

머신 러닝에는 다양한 옵티마이저가 존재한다

중요한 것은 다른 옵티마이저 들도 GD를 모두 기반으로 했다는 것

2. 경사하강법 (Gradient Descent)

개념

• 기울기(경사, gradient)를 이용하여 손실 함수의 값을 최소화 하는 방법
• 학습은 모델의 파라미터를 조정하는 것
  • 우리가 조정하고자 하는 값(변수)은 가중치(weight, 이하 w)와 바이어스(bias, 이하 b)
• 손실 함수를 w와 b에 관한 함수로 생각!

\[w = w - \alpha \times \frac{\partial L}{\partial w}\] \[b = b - \alpha \times \frac{\partial L}{\partial b}\]

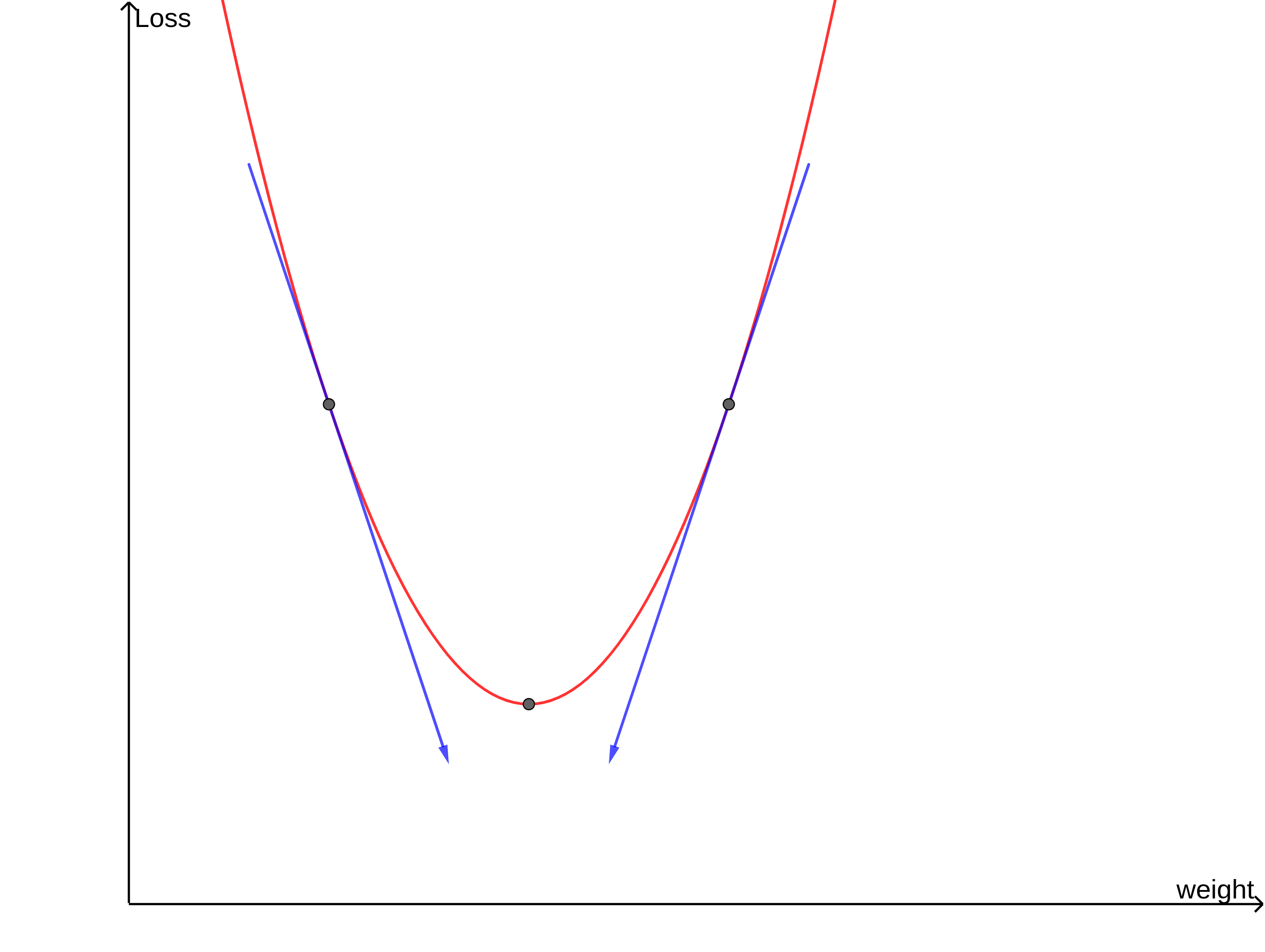
• w와 b를 다음과 같이 조정함
  • w : weight 가중치, b: bias 바이어스, ( \alpha ) : learning-rate 학습률
• 손실 함수의 기울기 값을 구하고 그 기울기 만큼을 학습률을 곱해서 빼주는 것
  • 위 방식을 여러번 반복해서 최종적으로 w가 최솟값을 찾도록 조정하는 것이 경사하강법

학습률(Learning rate)

• 하이퍼 파라미터(Hyper Parameter)의 한 종류
  • 파라미터에 영향을 미치는 파라미터

• w값이 움직이는 거리를 조절해주기 위해 사용

• 학습률이 너무 크다 = w가 이동하는 거리가 너무 크다
  • 손실 값이 커지는 방향으로 w가 조정될 가능성
• 학습률이 너무 작다 = w가 이동하는 거리가 너무 작다
  • w가 적합한 값으로 수렴하는데에 너무 오랜 시간이 걸림

3. 경사 하강법의 한계

1. 많은 연산량과 컴퓨터 자원 소모

• 경사하강법은 데이터(입력값) 하나가 모델을 지날 때마다 모든 가중치를 한 번씩 업데이트
  • 모델의 가중치가 매우 많다면 모든 가중치에 대해 연산을 적용하기 때문에 많은 연산량을 요구
• 모델을 평가할 때 정확도뿐만 아니라 연산량, 학습시간, 메모리 소비량 등도 평가 요소
  • -> 경사하강법의 치명적인 약점

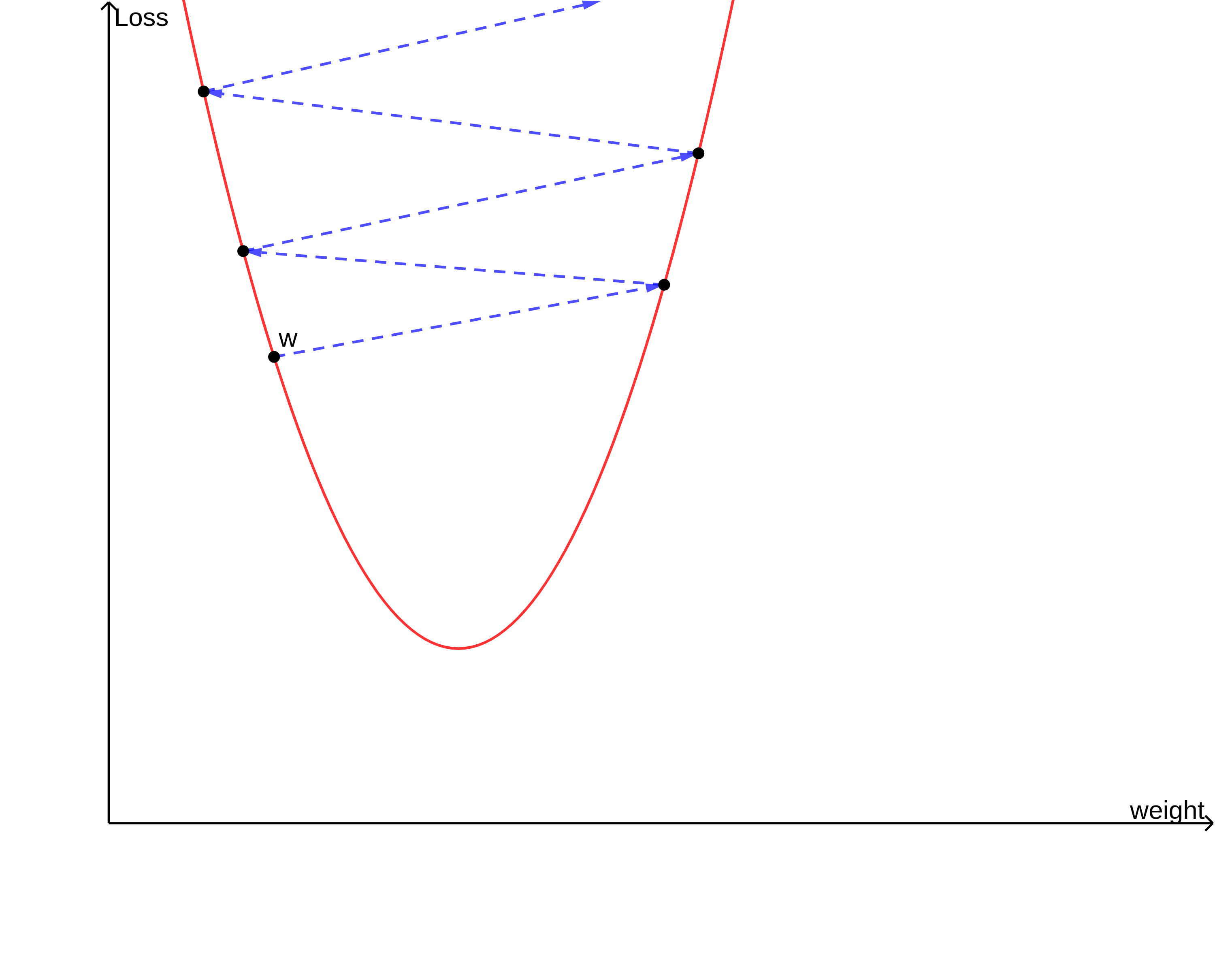
2. Local Minima(지역 극솟값) 문제

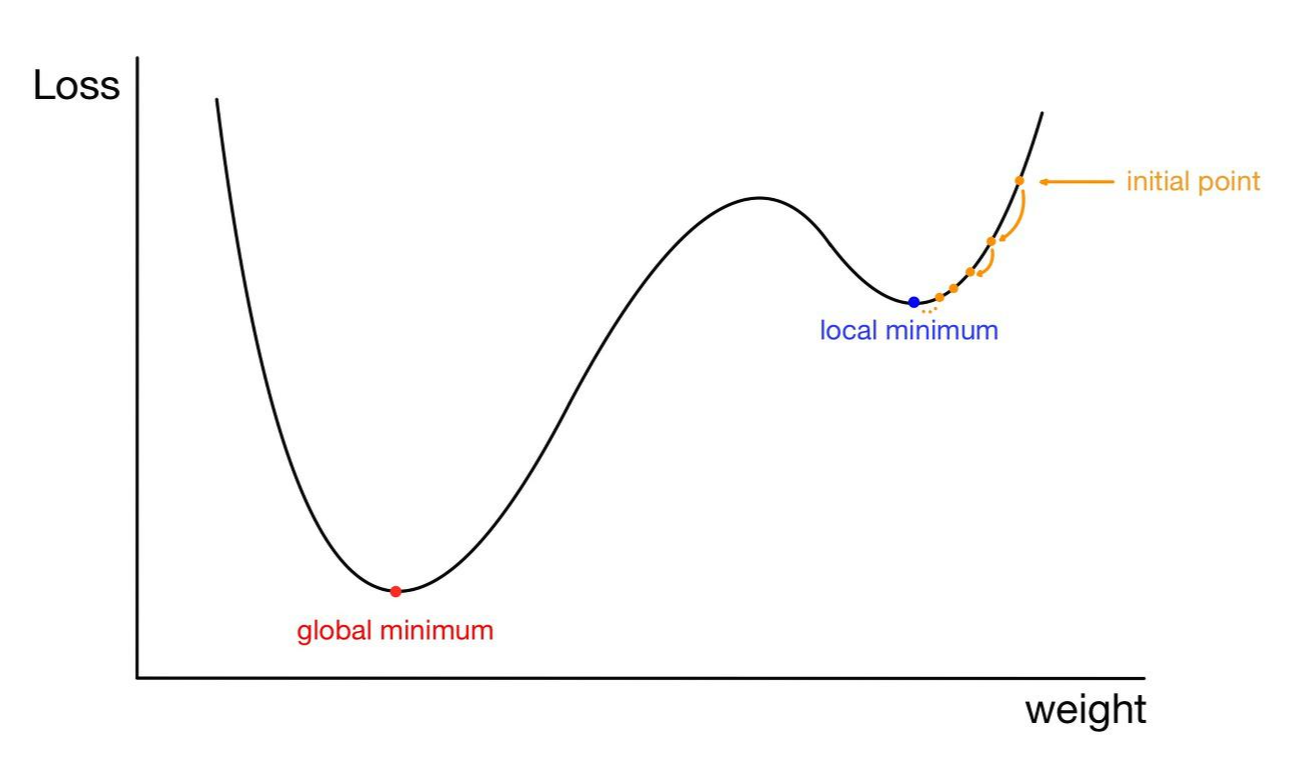
• 손실함수의 전역 최솟값이 아닌 지역 극솟값으로 수렴하는 문제
• 찾아나가야 할 가중치의 값은 손실 함수가 전역 최솟값(globla minimum)을 갖는점
  • (그림상 빨간 점)
• BUT 초기 시작점이 그림상의 노란 점이라면 전역 최솟값으로 향해 다가오는 도중에 지역 극솟값에 수렴해버릴 가능성
  • (그림상 파란 점)
    • 지역 극솟값에서의 손실 함수의 기울기 또한 0
    • w가 지역 극솟값에 갇혀 더 이상 업데이트되지 못할 수 있음

참고 사항

• 최근 머신러닝에서는 local minima문제가 흔히 발생하는 현상이 아니라는 의견도 있음
• 이유는 가중치의 개수가 많아질수록
  • 손실 함수의 critical point 대부분이 saddle point가 되고
    • local minimum이 될 확률이 매우 희박하기 때문

3. Plateau(고원) 현상

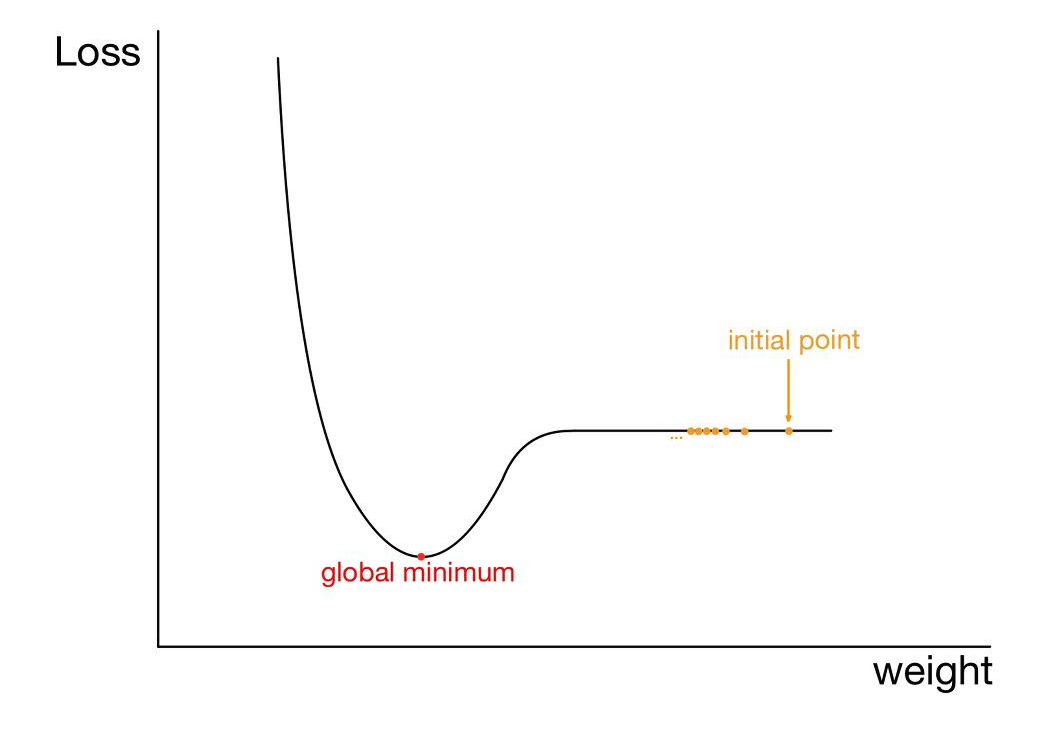
• 경사하강법은 기울기를 이용하는 방법
  • 가중치를 기울기가 큰 지점에서는 빠르게 수렴
  • 기울기가 작은 지점에서는 천천히 수렴
• BUT 위의 그림과 같이 평탄한 영역에 대해서는 기울기가 0에 수렴
  • 결국 가중치가 업데이트되지 못하고 전역 최솟값을 갖는 지점이 아닌 점에서 정지해버릴 위험
• 이 현상은 ‘local minima 문제’에 비해 상대적으로 자주 발생하는 현상

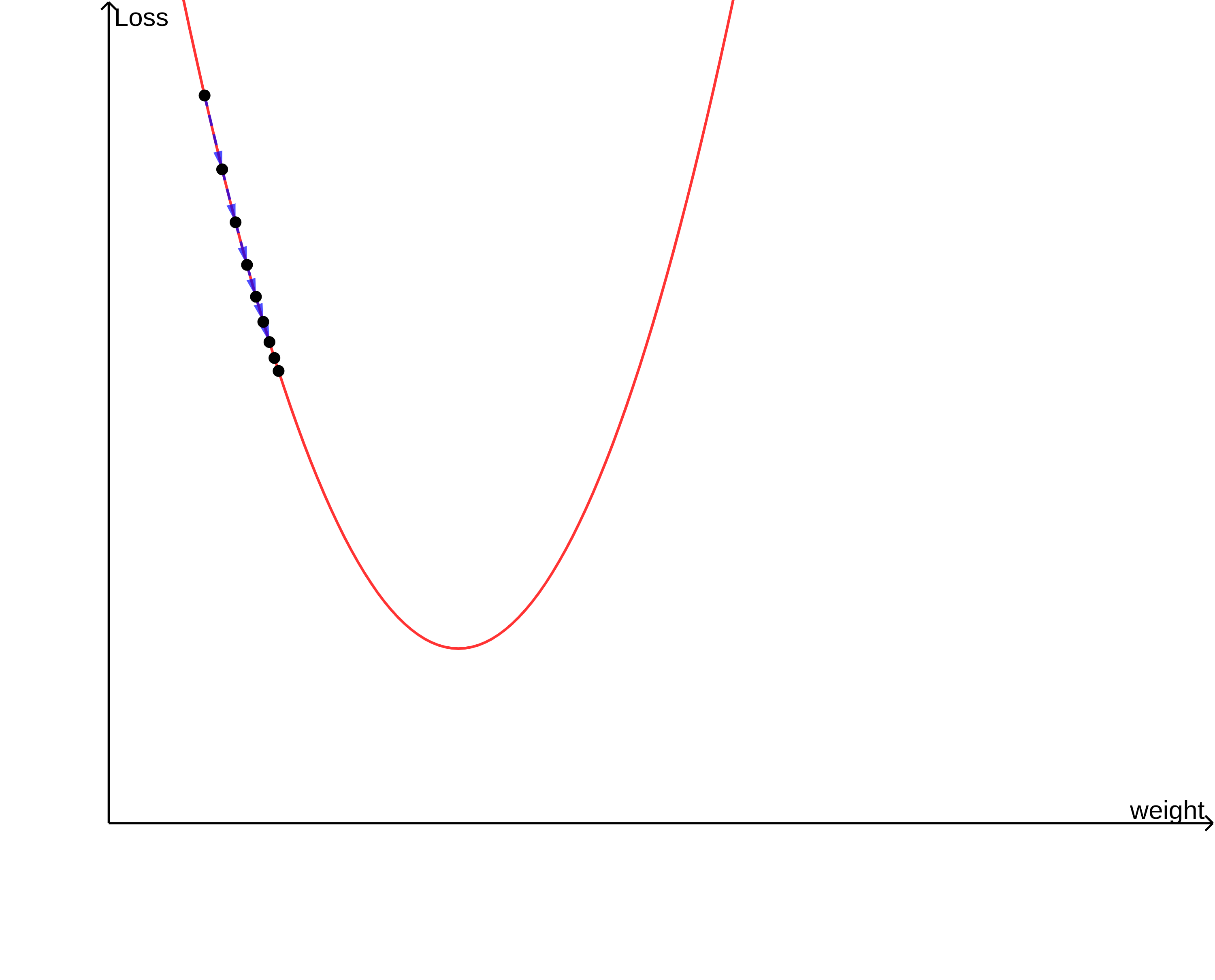
4. Oscillation(진동) 문제

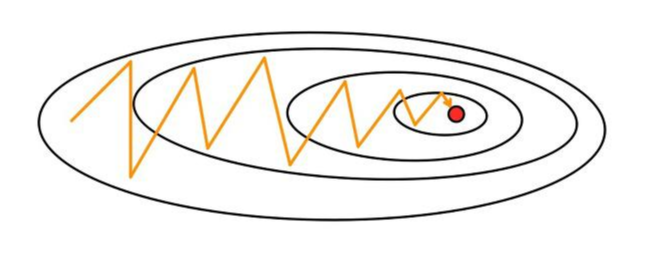
• 경사하강법은 현재 위치(시작 포인트)에서 최적값 방향으로 수렴하는 것이 아닌 기울기를 따라 수렴
• 만약 가중치들이 손실 함수에 미치는 영향이 크게 상이하다면
  • 위의 그림과 같이 크게 진동하며 최적값에 느리게 수렴
• 진동폭이 크다 = 가중치가 불안정하게 수렴한다
  • 만약 이동거리(step size)가 크다면 최적값에 수렴하지 못하고 발산해버릴 위험

참고 사항

• 가중치가 업데이트될 때 진동폭을 최대한 작게 만들어주는 것 또한 옵티마이저를 설정할 때 중요한 고려사항 중 하나

---

reference

• 머신러닝/딥러닝 공부 블로그

• 2024 2
• 2023 36
• 2022 15